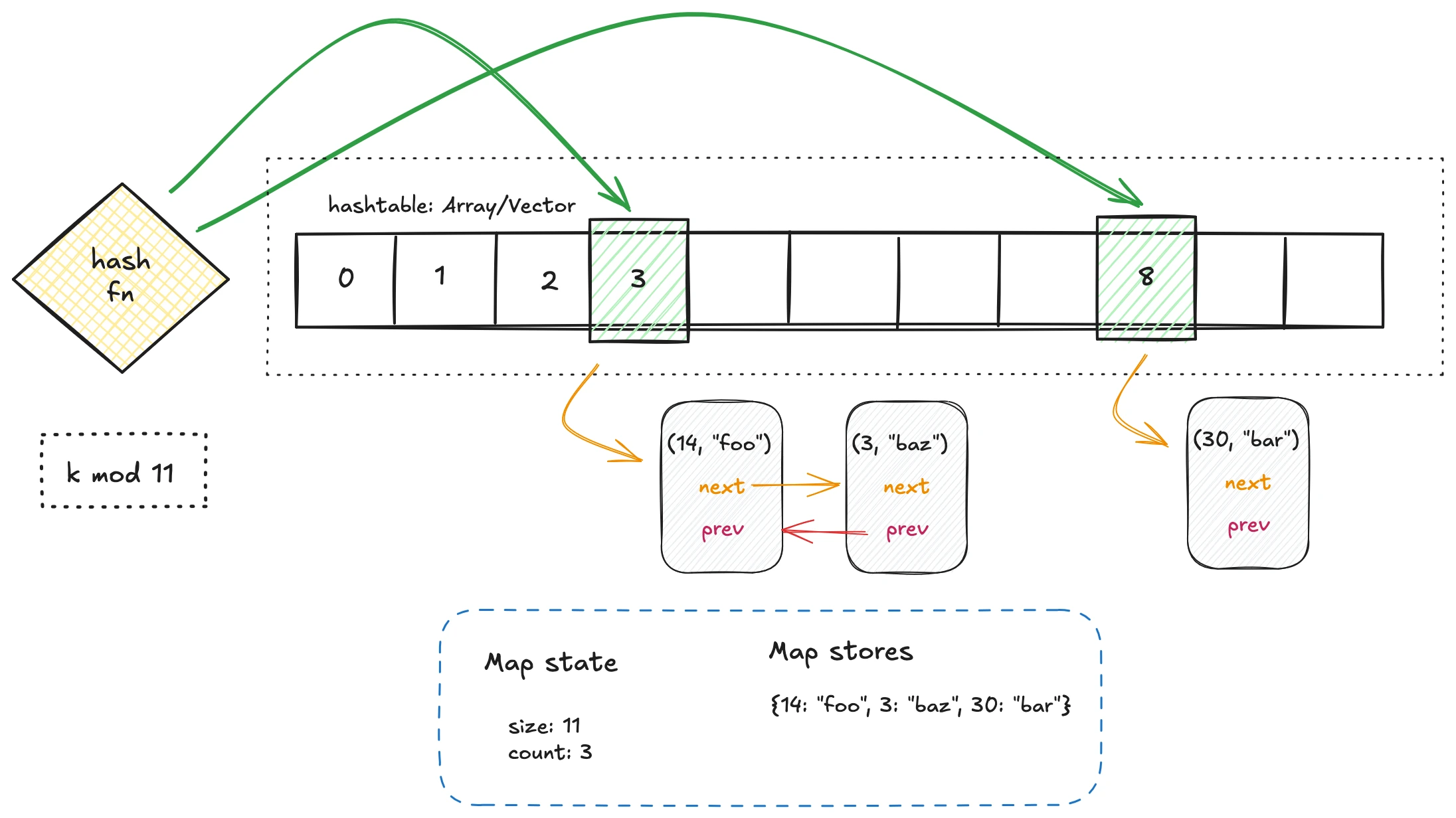
In the last article, we explored chaining, where collisions are resolved by attaching an external structure—typically a doubly linked list—to each bucket. This works, but it comes with a hidden cost. Linked lists scatter elements across the heap, turning each lookup into a sequence of random memory accesses. That destroys much of the performance advantage that arrays (or vectors) usually give us: tight, contiguous storage and cache efficiency.

Open addressing flips this philosophy on its head. Instead of pushing collisions outward into auxiliary structures, it insists that every key-value pair must live inside the array itself. No lists, no nodes, no extra indirection. At first glance, this seems elegant—one flat array, no messy pointers. Even better, the memory layout is cache-friendly, and linear scans often outperform linked structures despite doing “more work.”

But this internal simplicity comes with its own challenges. Once you commit to storing everything in the array, you now need careful strategies for:

• Probing: how to find the next open slot when a collision occurs.
• Deletion: how to remove elements without breaking probe chains (the infamous tombstone problem).
• Load management: how to keep the table from getting too crowded, since performance degrades rapidly as it fills.

In other words: open addressing hash tables offer elegance and speed in the best case, but force us to wrestle with subtleties in the worst.

Suppose you are building a location-based service like Yelp or DoorDash. A customer wants to find restaurants near them that match certain preferences. Their device provides a GPS location (latitude, longitude), and your app needs to quickly retrieve relevant restaurants in their vicinity.

But how do you efficiently query locations in a database? Traditional indexing methods, such as B-Trees, are optimized for sorting and searching one-dimensional data (e.g., numbers or strings). However, geographic locations exist in two dimensions, making proximity-based searches challenging.

A naive approach—scanning all locations and filtering those within a given radius—is inefficient at scale. To handle this, modern applications use geospatial indexes, which structure location data in a way that enables efficient retrieval of nearby points.

One such indexing method is geohashing, which encodes latitude and longitude into a compact, searchable format that allows for efficient range queries and neighbor lookups. In this article, we’ll explore how geohashing works, how to encode and decode locations, and how it is used in real-world applications like ride-sharing and food delivery services.

For instance, consider a pharmacy like CVS or Walgreens, which uses patients’ Social Security Numbers (SSNs)—a nine-digit unique identifier—to manage patient information. Not all patients visit the pharmacy regularly, so it would be inefficient to store data in a large array indexed by SSNs. Instead, dictionaries allow us to store, retrieve, or delete patient information efficiently, even when the SSNs are sparsely distributed.

What Are Promises? #

In JavaScript, Promises are objects that represent the eventual completion (or failure) of an asynchronous operation and its resulting value. They provide a powerful way to manage asynchronous code, enabling developers to write cleaner and more maintainable logic.

Promises allow us to associate handlers for both the success and failure of an asynchronous operation. By treating asynchronous code similarly to synchronous code, they reduce the complexity and improve the readability of workflows that would otherwise be riddled with convoluted callbacks—commonly referred to as “callback hell.”

I recently moved my blog from Jekyll, a Ruby-based static site generator, to Hugo, a popular alternative built in Golang. In this article, I’ll walk through the rationale behind this migration, share the steps I took, and include a few custom code snippets I created along the way. This is not intended as a tutorial on setting up a blog with Hugo — there are plenty of excellent videos and documentation on Hugo’s site for that. Instead, I’ll focus on my experience, insights, and the lessons learned that may be helpful for anyone considering a similar transition.

You could find an older version of my site at archive.