Understanding Skip lists
Could skipping through data be faster than balancing trees? Dive into the fascinating mechanics of skip lists, where probability shapes efficiency.
Suppose you have a sorted collection of elements and need to perform add, delete, and search operations efficiently. Skip lists offer an efficient, probabilistic approach to these operations, achieving an average time complexity of \(O(\log{n})\) for search, insertion, and deletion. While other data structures, such as red-black trees and AVL trees, can provide the same \(O(\log{n})\) efficiency guarantees in both the average and worst cases, skip lists have the advantage of being simpler to implement and understand.
With basic data structures like sorted arrays, you can search for elements in \(O(\log{n})\) time using binary search. However, insertion and deletion require shifting elements, leading to \(O(n)\) time complexity for these operations. Conversely, linked lists allow efficient \(O(1)\) insertions and deletions once the target location is found, but finding that location requires \(O(n)\) time in the worst case.
How Skip Lists improve efficiency #
So, how do skip lists achieve \(O(\log{n})\) efficiency for all three operations? Skip lists accomplish this by introducing multiple levels, each serving as an “express lane” that allows you to skip over sections of the list. The highest levels contain fewer nodes, allowing you to make large jumps, while the lowest level contains all nodes, allowing for precise adjustments when needed. This structure enables fast traversal through the express lanes and, when necessary, you can exit to a lower level for finer-grained searching.
To make the analogy clearer, think of these levels as a series of express lanes on a highway. As you travel along an express lane, you occasionally find exits that let you drop down to slower lanes with more nodes, offering greater detail for precise adjustments. This balance of speed and accuracy allows skip lists to achieve efficient search, insert, and delete operations.

Fig 1. An example Skip List
Note on Bidirectional traversal
For simplicity, we assume here that skip lists contain only forward links, though it’s possible to implement bidirectional (backward) links. Without (sidenote: A helpful heuristic in this case would let us know approximately how much skips away target node is. ) heuristics or specific knowledge of data distribution, however, it’s often hard to predict if moving backward would be more efficient than moving forward. Thus, a simple forward-only skip list remains optimal for most use cases.
Now, let’s take a look at initializing a skip list.
Initializing a Skip List #
Like a linked list, a skip list also consists of “nodes” and a primary data structure that encapsulates the nodes, providing insert, delete, and search operations. Each node in a skip list, represented here as SkipListNode, stores a value and a forward list of pointers to the next nodes at various levels. This list enables the “express lanes” that allow for efficient traversal and manipulation of the list.
![A diagram depicting internal state of a skip list - [cur_level: (int), max_level: (int), probability: (float), Node: (SkipListNode: (value: int, forward: list[SkipListNode]))]](/articles/understanding-skiplists/SkipListClassDiagram.webp)
Fig 2. Skip List state
Components of SkipListNode
value: Stores the value or data held by the node.forward: A list of pointers, where each index corresponds to a level in the skip list. At each level, it points to the next node at that level or remains None if no such node exists.
Components of the SkipList Structure
The SkipList class itself maintains key attributes that govern its behavior:
head: A SkipListNode instance that serves as the starting point of the skip list at all levels. Its forward list has a length equal to max_level.max_level: Specifies the maximum level height for the skip list, which caps the number of levels any node can have.cur_level: Tracks the highest level currently in use within the skip list, which grows as nodes are added with higher levels.probability: Defines the probability factor used to determine the level height of each new node, influencing the list’s balance.
1class SkipListNode:
2 def __init__(self, value: int, level: int):
3 self.value = value
4 self.forward = [None] * (level + 1)
5
6class SkipList:
7 def __init__(self, max_level: int, probability: float):
8 self.head = SkipListNode(None, max_level)
9 self.cur_level = 0
10 self.max_level = max_level
11 self.probability = probability
12
13 def _random_level(self) -> int:
14 level = 0
15 while random.random() < self.probability and level < self.max_level:
16 level += 1
17 return level
Next we can look into the search operation, we start with search because the same logic is used in insert and delete.
A little bit on what role probability plays
Till now we talked about the levels in skip lists. One could carefully choose which elements to put on the higher levels
if we know the proximity of other elements. In practice when we have inserts and deletes with no information on the
distribution of data we will have no way to know what level is optimal for a node. Here is where probability comes into
play. We can assign the level of a node randomly provided the probability for each node decreases exponentially.
The level structure is also such that if a node is at level \(k\) it has pointers to forwards for all levels less than \(k\).
So far, we’ve discussed levels in skip lists. Ideally, we could manually select which elements to place on higher levels if we had information about the distribution or proximity of elements. However, in dynamic scenarios where insert and delete operations occur without any predefined data distribution, it’s difficult to predict an optimal level for each new node. Probability provides an elegant solution here.
By using a random level assignment governed by a probability factor, we ensure that the number of nodes decreases exponentially with each increasing level. This probabilistic approach keeps the skip list balanced on average, allowing it to maintain efficient \(O(\log{n})\) performance across search, insert, and delete operations.
Additionally, each node’s level is structured such that if a node is at level \(k\), it has forward pointers for all levels below \(k\). This ensures seamless traversal between levels during search operations.
Search operation in Skip Lists #
The search operation in a skip list forms the foundation for insert and delete operations as well, so let’s cover it first.
In a skip list, we begin the search from the head node using a pointer called current. current has a list of forward pointers that allow traversal across different levels. Starting from the highest active level (cur_level), we examine each forward pointer on that level. If the forward pointer’s value is less than our target value, we advance current to this forward node and continue on the same level. If a forward node’s value exceeds the target value, we drop down one level and repeat this process.
This traversal continues until one of two conditions is met:
- We reach a node whose forward pointer value matches the target value (indicating success).
- We reach level 0 and a forward pointer exceeds the target, or points to
None(indicating the target is not present in the list).
Below is a python implementation of search.
1def search(self, target: int) -> bool:
2 current = self.head
3 # Search each level till the next has esxceeded target. Once exceeded go down to lower level.
4 for level in range(self.cur_level, -1, -1):
5 while current.forward[level] and current.forward[level].value < target:
6 current = current.forward[level]
7 current = current.forward[0]
8
9 return current and current.value == target
We can look at insert next.
Insert operation in Skip Lists #
The insertion process in a skip list can be broken down into three main steps:
- Identify the Insert Position: Find the correct position for the target value, marking nodes whose forward links will need to be updated to point to the new node.
- Create a New Node: Instantiate a new SkipListNode and assign it a level based on the probability factor.
- Reconnect Forward Links: Insert the new node by updating the forward links of the marked nodes.
Step 1: Find the Insert Position #
Finding the insert position for the target value closely resembles the search operation. Starting from the highest active level, traverse each level until you reach the correct position where the target should be inserted. As you go, keep track of the nodes whose forward pointers will need updating to accommodate the new node. These are either the last nodes on that level or the node that will directly precede the new node on each level.
Step 2: Create a New Node #
Once the position is identified, create a new SkipListNode with the specified target value. Determine the node’s level using the probability factor, which governs the likelihood of each node appearing on higher levels.
Step 3: Reconnect Forward Links #
Finally, reconnect the marked forward links to the new node. Starting from the node’s assigned level down to level 0, adjust each marked node’s forward pointer to include the new node. This effectively “weaves” the new node into its position at every level, integrating it fully into the skip list structure.
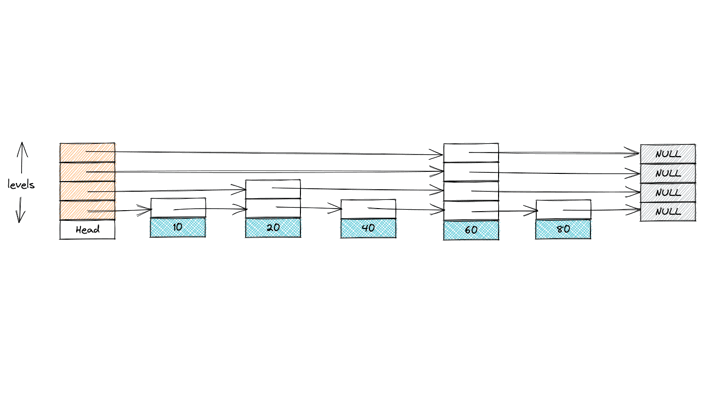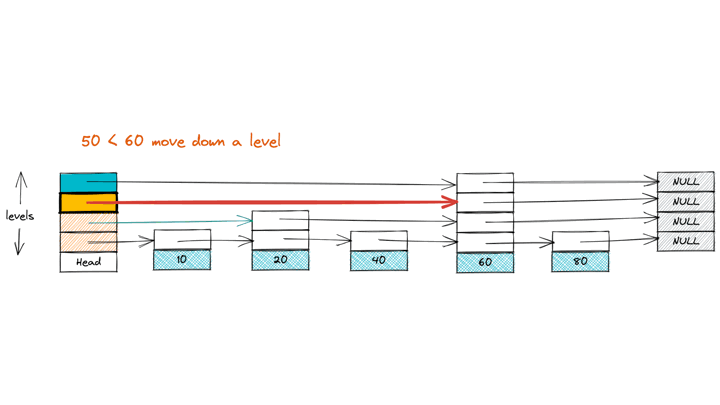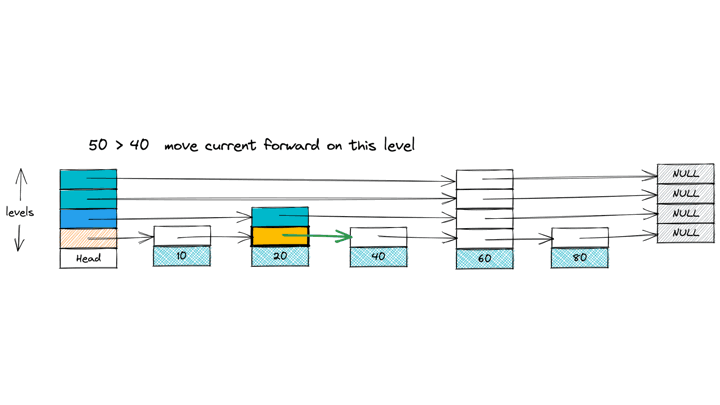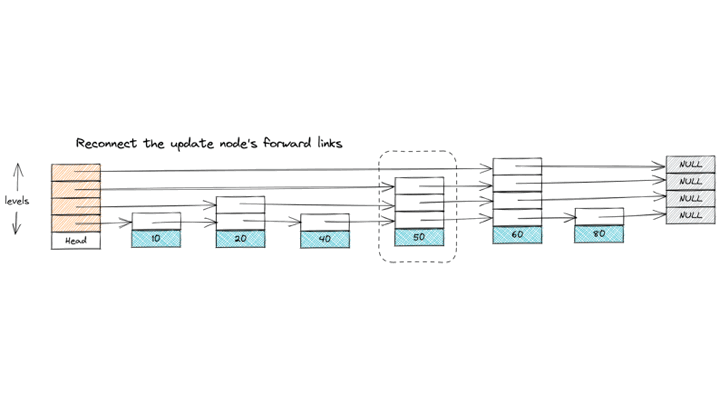
Fig 3. An example of an insert operation on Skip List
1def insert(self, val: int) -> None:
2 update = [None] * (
3 self.max_level + 1
4 ) # Used to track all nodes whose next would be new val
5 current = self.head
6
7 # Traverse and mark each node which should be updated
8 for level in range(self.cur_level, -1, -1):
9 while current.forward[level] and current.forward[level].value < val:
10 current = current.forward[level]
11 update[level] = current
12
13 # Assign a level to the new value
14 new_level = self._random_level()
15
16 if new_level > self.cur_level:
17 for i in range(self.cur_level + 1, new_level + 1):
18 update[i] = self.head # Propagate head nodes to higher levels
19 self.cur_level = new_level
20 new_node = SkipListNode(val, new_level)
21
22 for i in range(new_level + 1):
23 new_node.forward[i] = update[i].forward[i]
24 update[i].forward[i] = new_node
Delete operation in Skip Lists #
The delete operation in a skip list closely resembles the insert operation and can be broken down into two main steps:
- Identify the delete position: Locate the target value in the skip list, keeping track of nodes whose forward links will need updating to bypass the target node.
- Reconnect forward links: Remove the target node if it exists and reconnect the preceding nodes’ forward links to the nodes that follow the target.
Step 1: Identify the Delete Position #
Finding the position of the target value for deletion follows the same logic as the search operation. Starting from the highest active level, traverse each level of the skip list, tracking nodes whose forward pointers will need updating to remove the target node. These nodes are either the last ones on each level or the nodes that directly precede the target node on each level.
The skip list will delete only the first occurrence of the target value found. If the target value is not present in the list, the operation is aborted.
Step 2: Reconnect Forward Links #
Once the target node is identified, update the forward links of all preceding nodes to skip over the target node, effectively removing it from each level where it exists. After updating links, clean up any higher levels in the skip list that are now empty.
Here’s a Python example of how this deletion process works:
1def delete(self, target: int) -> bool:
2 update = [None] * (self.max_level + 1) # Used to track all nodes whose next should be updated.
3 current = self.head
4
5 for level in range(self.cur_level, -1, -1):
6 while current.forward[level] and current.forward[level].value < target:
7 current = current.forward[level]
8 update[level] = current
9
10 current = current.forward[0]
11 # Value is not found
12 if not current or current.value != target:
13 return False
14 # Update the forward links to skip/bypass target node
15 for i in range(self.cur_level + 1):
16 if update[i].forward[i] != current:
17 break
18 update[i].forward[i] = current.forward[i]
19
20 # Clean up any left over levels that are empty
21 while self.cur_level > 0 and self.head.forward[self.cur_level] is None:
22 self.cur_level -= 1
23 return True
Closing notes: When to use Skip Lists #
Skip lists are a probabilistic data structure that balances performance and simplicity. They offer efficient operations with average-case time complexity of \(O(\log{n})\) for search, insertion, and deletion, but without the strict balancing requirements of red-black or AVL trees. Below are some scenarios where skip lists may outperform other structures like red-black trees, AVL trees, or hash tables: Range Queries
- Efficient range searches: Skip lists excel in range queries, as they allow for quick traversal over nodes within specified bounds. By leveraging the multi-level structure, skip lists can efficiently identify all elements within a given range.
- Real-time applications: In database systems or network applications where efficient range queries are crucial, skip lists provide an effective and straightforward option.
Ordered Data
- Inherent order maintenance: Skip lists maintain elements in sorted order by design, which makes them suitable for applications needing ordered traversal or lookups for successive or preceding elements.
Simple Implementation
- Ease of coding and maintenance: Unlike self-balancing trees (e.g., red-black or AVL trees) that require complex rotations or rebalancing logic, skip lists achieve balance through probabilistic leveling. This feature simplifies the codebase and reduces maintenance complexity, making skip lists relatively easy to implement and debug.
Limitations of Skip Lists
Despite their benefits, skip lists come with trade-offs:
- Performance Variability: Skip lists offer excellent average-case performance but do not guarantee the same worst-case efficiency as balanced trees. In rare cases, skip lists may degrade to linear time if level distribution is unbalanced.
- Increased Memory Usage: To enable their multi-level structure, skip lists require additional memory to store pointers at each level, which can increase space usage compared to simpler structures.
You can see the full implementation here.